سی امین کنفرانس اپتیک و فوتونیک ایران و شانزدهمین کنفرانس مهندسی و فناوری فوتونیک ایران نهم تا یازدهم بهمن ماه 1402 به میزبانی دانشگاه دامغان به‌شکل حضوری برگزار خواهد شد.

داستان یافتن رابطه وابستگی ضریب شکست  ( شیشه های اپتیکی - محیط های اپتیکی شفاف برای طیف نور ) به طول موج بر اساس روابط تجربی و محاسباتی  ( مراجعه کنید به Models for Fitting Refractive Index vs Wavelength ) به سال 1836 باز می گردد. گروهی بر اساس معادله کوشی Cauchy تقریبی را معرفی کردند.

گروه دیگری مدل مشابهی به نام مدل Conrady  معرفی کردند. ( این مدل اولین بار در کتاب Applied Optics and Optical Design  نوشته Conrady  معرفی شد )

\[ Conrady Equation \;\;\;\; n(\lambda )=A+\frac{B}{\lambda^2}+\frac{C}{\lambda^{3.5}}\]

مدل های دیگری همچون HelmHoltz و Hartmann نیز ارائه شدند.

\[ Hartmann Equation \;\;\;\; n(\lambda )=A+\frac{B}{(C-\lambda)^D}\]

مدل Hezberger رابطه بسیار کارآمدی برای پهنای طیفی بزرگ را در اختیار ما قرار می دهد. معمولا در نرم افزارهای اپتیکی از این مدل با 5 یا 6 جمله استفاده می شود.

\[ n(\lambda )=A+B\lambda^2+C\lambda^4+D\lambda^6+\frac{E}{(\lambda^2-0.028)}\]

شرکت Schott بر اساس سری لورانت Laurent Series ، مغادلات چند جمله ای مفیدی را معرفی کرد. هر چه تعداد جملات مورد استفاده از این چند جمله ای بیشتر باشد ، نتیجه دقیق تر است.

\[ n(\lambda )^2=A+B\lambda^2+\frac{C}{\lambda^2}+\frac{D}{\lambda^4}+\frac{E}{\lambda^6}+\frac{F}{\lambda^8}\]

فرم کلی معادلات Sellmeier به صورت زیر است

\[ n(\lambda )^2-1=\sum_{i}^{} \frac{A_{i}\lambda^2}{\lambda^2-\lambda_{i}^{2}}\]

معمولا در نرم افزارهای اپتیکی از 5 جمله اول رابطه Sellmeier استفاده می شود.

با تصحیح معادلات Sellmeier برای رسیدن به دقت بیشتر روابط ترکیبی ( اضافه شدن جملاتی از Schott و Herzerberg ) به معادله اصلی مدل Sellmeier 2 معرفی و مورد استفاده قرار می گیرد. مدل هایی مانند KINGSLAKE و MISC هم معرفی شده اند که کاربرد زیادی ندارند.

با توجه تجربی و محاسباتی بودن رابطه ها مهم دقت و تفاضل مقدار بدست آمده با مقدار واقعی در آزمایشگاه است. هر مدلی در بازه طیفی مشخصی برای هر شیشه ای دقت و تفاضل یکسانی ندارد. هدف یافتن معادله ای ساده ( برای استفاده در محاسبات کامپیوتری ) با دقت بالا است.

نمودار ضریب شکست - طول موج را برای Fused Silica

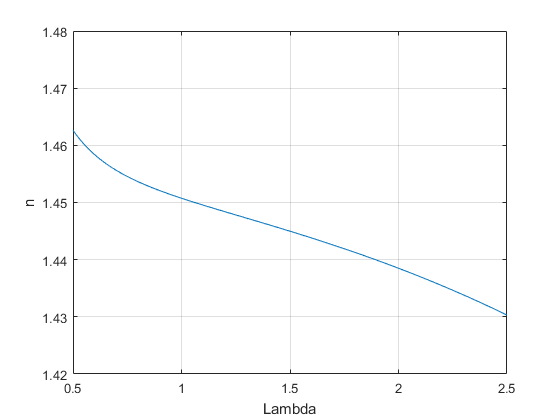
نمودار سرعت گروه - طول موج را برای Fused Silica

\[ v_{g}=\frac{c}{n-\lambda(dn-d\lambda)}\]

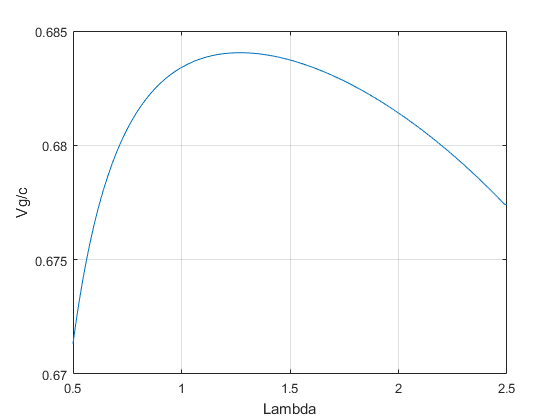
نمودار پاشیدگی سرعت گروه Group Velocity Dispersion - طول موج را برای Fused Silica

\[ D=\frac{1}{c\lambda}(\lambda^{2} \frac{d^{2}n}{d\lambda^{2}})\]

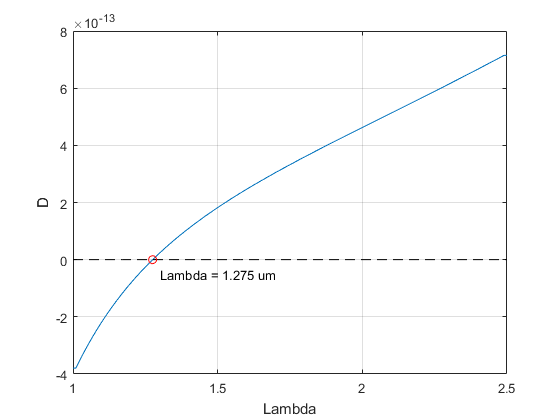
| جهت هماهنگی برای آموزش اپتیک ، فوتونیک و برنامه نویسی محاسباتی با شماره 02191307193 تماس حاصل نمایید.